melreams.com

In a recent post I mentioned having read an article about passing programming interviews that said it was important to be able to write a breadth-first search and to understand how hash maps work. I covered hash maps last time, so this time let’s talk about breadth-first searches.

The first question is what on earth is a breadth first search? It’s a way of searching a tree structure. in a breadth-first search, you look at all the nodes at a particular ‘level’ of the tree before looking at anything in the next level. Another way you can do it is depth-first, where you follow each node’s children down and down until you run out of children, then go back up to the next child node you haven’t already visited and follow it’s children down until you run out again, and so on until you’ve visited all the nodes in the tree.

This is definitely a case where a picture is worth 1000 words. Here’s the order you visit nodes in a breadth-first search:

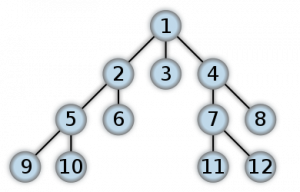
and here’s the order in a depth first search:

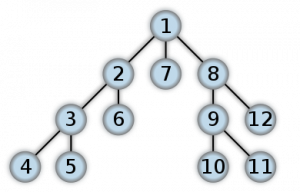
Great, what’s a breadth-first search for? According to wikipedia it’s good for a bunch of problems in graph theory that I totally don’t understand, and some more understandable stuff like finding the shortest path between two nodes in a tree and serializing a binary tree in such a way that you can easily deserialize it.

So how do you do a breadth-first search anyway?

bijulsoni has graciously provided an example in their article Introduction to Graph with Breadth First Search(BFS) and Depth First Search(DFS) Traversal Implemented in JAVA on Code Project. If you’re interested, that code is provided under The Code Project Open License (CPOL) 1.02, which basically states that you can do whatever you like with the code but don’t come crying to them if it doesn’t work.

Here’s a breadth-first search:

 
public void breadthFirstSearch() { 
    //BFS uses Queue data structure 
    Queue q=new LinkedList(); 
    q.add(this.rootNode); 
    printNode(this.rootNode); 
    rootNode.visited=true; 
    while(!q.isEmpty()) { 
        Node n=(Node)q.remove(); 
        Node child=null; 
        while((child=getUnvisitedChildNode(n))!=null) { 
            child.visited=true; 
            printNode(child); 
            q.add(child); 
        } 
    } 
    //Clear visited property of nodes 
    clearNodes(); 
} 

and to compare, here’s how a depth-first search works:

public void depthFirstSearch() {
    //DFS uses Stack data structure
    Stack s=new Stack();
    s.push(this.rootNode);
    rootNode.visited=true;
    printNode(rootNode);
    while(!s.isEmpty()) {
        Node n=(Node)s.peek();
        Node child=getUnvisitedChildNode(n);
        if(child!=null) {
            child.visited=true;
            printNode(child);
            s.push(child);
        } else {
            s.pop();
        }
    }
    //Clear visited property of nodes
    clearNodes();
}

The complete, runnable code can be downloaded from the article linked above if you’d like to run it yourself. getUnvisitedChildNode() does what you would expect, so I left it out to save space. What I find really interested about the breadth-first and depth-first algorithms is that they’re practically identical except for the different data structures used to hold the nodes we’re working on. The simple change from a queue (where you add items to the end and remove items from the head) to a stack (where you both add and remove items from the end) is all it takes to change a breadth-first search to a depth-first search.

Now we all know how a breadth-first search (and a depth-first search as a bonus) works. You can safely forget the details, secure in the knowledge you can look it up if you need to :)