Programming interview concepts are back! You can find the rest of those posts under the how does it work? tag.
Before we talk about how a binary tree works, we should probably talk about what it is. A binary tree is just a tree data structure where each node has at most two children. Thank you wikipedia :) There’s nothing preventing you from making a tree where each node has more than two children, it just wouldn’t be a binary tree. A tree, binary or not, isn’t necessarily sorted either.
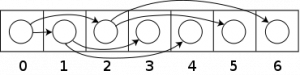
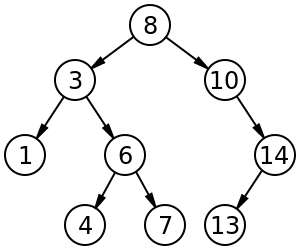
A tree works a lot like a linked list, each node has references to its children, allowing you to walk down the tree. You can also implement a binary tree using a plain old array (see the picture to the right), but that can waste a lot of space if your tree isn’t both balanced and complete. Balanced, when we’re talking about trees, means both sides have the same number of nodes (or at least close to the same number), and complete means that on each ‘level’ all the nodes are filled in. In the example binary tree below, it’s not balanced because one side has 5 nodes and the other only has 3, and it’s not complete because there’s one node missing on the third level and two or three nodes missing on the fourth, depending on whether your definition of ‘complete’ allows for any leaf nodes on the right-most end of the last level of the tree to be missing. That doesn’t actually have much to do with the rest of this post, I just thought it was nifty :)
A binary search tree is a special case of tree where each node has 0-2 children and the nodes are sorted so that you can perform a binary search. In my post about how a binary search works, I mentioned that binary trees aren’t actually the fastest data structure to use for a binary search because it’s hard to balance a binary tree.
How do you balance a binary tree, anyway? Well, if you sorted all of your items before you added them to your tree, then you could start with the item in the middle, then add the middles of the two halves, then add the middles of those halves, and so on until you’ve added everything. That method only works if you already have all of the items you’re going to put in the tree and can be bothered to sort them, though. What do you do if you need to add more items later?
Basically you need to re-arrange your tree until it’s balanced (or at least close enough) again. Some of the ways you can do this are with self-balancing trees like red-black trees or AVL trees. Both of those trees add some extra data to each node to help it both figure out if it’s out of balance and get it back into balance.
In red-black tree, the extra data is the “colour” of the node. Because there are only two colours this only takes one extra bit to store. The colours, by the way, are totally arbitrary so don’t knock yourself out trying to understand the deeper meaning behind them :) According to one of the inventors of the red-black tree, red and black were the colours that looked the best on the laser printer they had available, which they were eager to use since they worked at Xerox PARC where the laser printer was invented.
A red-black tree uses the following rules to keep itself from getting badly unbalanced:
- A node is either red or black.
- The root is black. This rule is sometimes omitted. Since the root can always be changed from red to black, but not necessarily vice versa, this rule has little effect on analysis.
- All leaves (NIL) are black.
- If a node is red, then both its children are black.
- Every path from a given node to any of its descendant NIL nodes contains the same number of black nodes. Some definitions: the number of black nodes from the root to a node is the node’s black depth; the uniform number of black nodes in all paths from root to the leaves is called the black-height of the red–black tree.
Red-black trees do some funny business with their nodes – what you would think of as a leaf node actually has two leaves that are always black and don’t contain any information. If you’re wondering “well if they’re always black and don’t contain any information, can’t I just pretend they exist and not waste memory on them?” the answer is yes, you can totally do that.
The thing with the pretend leaves is that you need them for the third rule about leaves always being black. When you add a node to a red-black tree, you don’t add it as a real leaf, you add it to the closest node that has a value and then pretend it has black leaves. For the first couple of nodes after the root, this is super simple – the root is black, the new nodes are red, their pretend leaves are black, and everything is good. If you have more than a couple nodes in your tree, things get complicated. That’s where you break out rotations. Because this post is already pretty long I’m going to refer you back to the wikipedia article on red-black trees and this youtube video by OnlineTeacher. Normally I kind of loathe videos, but the pictures in that one are actually really helpful. Tree rotations are one of those things that are really simple when you can see them and really, really confusing when you have to describe it in words. The short version is that because of the way binary search trees are arranged, you can rotate notes back and forth around the root of your subtree, which is going to make precisely no sense unless you already know what I’m talking about :)
My understanding of AVL trees is that they work on largely similar principles to red-black trees but because they’re more rigidly balanced they’re faster on retrieval but slower on updates. Everything is a tradeoff.
And finally, because I keep hearing about it as an interview question, how do you reverse/invert a binary tree?
First, let’s define what reversing a binary tree actually means. Before I looked this up I thought it had something to do with swapping the root and the leaves, which makes no sense because tree structures normally have only one root node. It turns out the question actually means swapping the left and the right children of each node.
From my quick bout of googling, it sounds like a fairly simple recursive algorithm to walk the tree and swap each node’s right child for its left child. Now you know.
As you might have noticed, my research here centered pretty heavily on wikipedia so if I messed anything up, tell me about it in the comments.